Simple Harmonic motion:
![]()
a linear restoring force, the force is directly proportional to the displacement
and in the opposite direction
frequency/period/angular frequency
oscillation, cycle, vibration,
equilibrium (rest) position
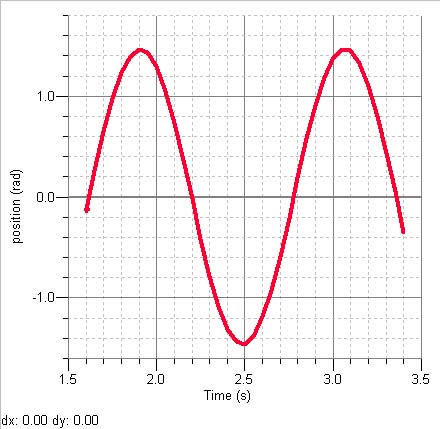
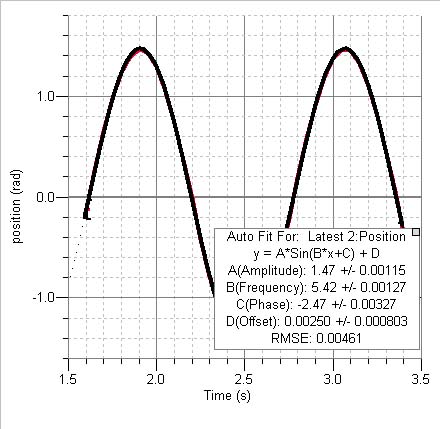
Amplitude (linear/angular)
axis of symmetry
simple pendulum
equations/limitations
Resonance
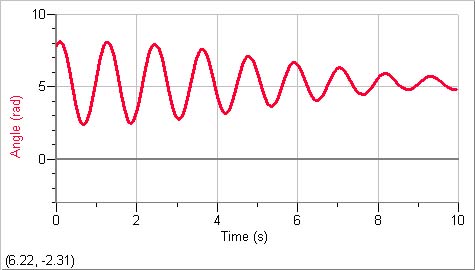
damping
-transverse
-longitudinal (translational)
rarefaction/compression
-torsional (rotational)
angular frequency ![]()
cycle/oscillation/vibration:
one complete motion tothe point where the motion starts to repeat
3 types of SHM:
1) longitudinal
2) transverse
3) torsional
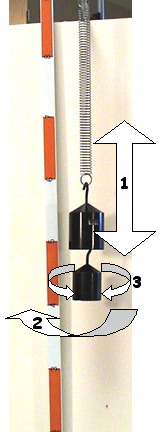

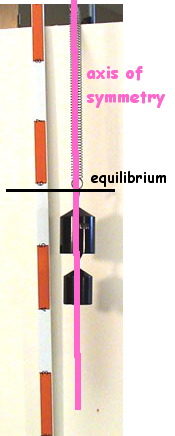
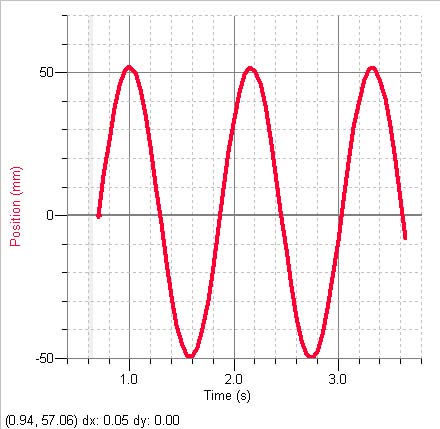
Longitudinal: the mass is displaced parallel (or antiparallel) to the axis of symmetry or the amplitude is along the axis of symmetry creating areas of compression and rarefaction; amplitude is measured as a distance



![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()